Per poter meglio studiare il potere emissivo di un corpo è stato necessario costruire un modello che riproducesse con buona approssimazione le caratteristiche di un corpo nero ideale.
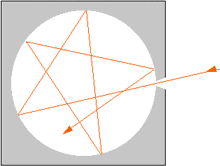
A tale scopo si è considerata una cavità rivestita internamente di nerofumo, materiale assorbente; tale cavità possiede un piccolissimo foro su una parete, di dimensioni trascurabili rispetto a quelle della cavità.

Tale configurazione permette alla cavità stessa di digerire l'eventuale radiazione che penetra dal foro, con possibilità praticamente nulle che il raggio entrato riesca ad uscire.
In realtà dobbiamo sottolineare che il corpo emette radiazione dopo la termalizzazione. Tuttavia l'emissione è di natura completamente diversa rispetto alla radiazione che incideva inizialmente.
L' emissione di corpo nero, infatti, dipende esclusivamente dalla temperatura efficace del corpo stesso.

Per i fisici di fine secolo fu naturale pensare alla cavità sopracitata come costituita da atomi di Thomson. Questi, per un effetto di risonanza - efficace solo ad alcune frequenze - sono in grado di contribuire alla termalizzazione della radiazione.
Per coprire tutte le frequenze, così come deve appunto fare un corpo nero, è necessario associare un numero altissimo di atomi - intesi come oscillatori armonici - in modo che dal loro accoppiamento si formi un sistema di termalizzazione più efficace.

Studiando l'emissione dei corpi i fisici Stefan e Boltzmann riuscirono ad estrapolare sperimentalmente una semplice funzione in grado di esprimere la potenza emessa per unità di superficie da un corpo nero.

La densità di energia nella cavità dopo la termalizzazione sarà una sommatoria - integrale - di energie relative ad una determinata frequenza ν e temperatura T.

U=∫+∞0u(ν,T)⋅dν→U=U(T)

Da cui si deduce che la densità di energia è in funzione della sola temperatura. La legge di Stefan, sull'energia totale emessa da un corpo nero nell'unità di tempo, afferma appunto che tale potenza è proporzionale a T⁴, con costante di proporzionalità σ, detta costante di Stefan-Boltzmann.

E=σ⋅T4 σ=5.67⋅10−8Wm2K4

‣ L'emissione di corpo nero per irraggiamento in un ambiente reale:

Q=eσA(T4c−T4amb)Δt

Dove e è l'emissività caratteristica (costante), A l'area del corpo e Δt il tempo di emissione.

‣ La legge di Fourier della conduzione:

Q=h⋅Ad⋅ΔT⋅Δt

In cui la quantità di calore Q è condotta in un intervallo di tempo Δt tra due zone a contatto con ΔT diverse, separate da un materiale omogeneo e isotropo di costante di conducibilità termica h nota, di area A e di spessore d.

Wien si occupò di come avveniva l'equilibrio termico tra la radiazione incidente e l'interno della cavità. Egli considerò le pareti interne come specchi ideali, incapaci di riflettere completamente la radiazione. Ciò che il fisico ipotizzava era quindi un urto non perfettamente elastico.
Dopo calcoli complessi, Wien giunse alla formulazione della legge omonima:

u(ν)=ν3⋅F(νT)

A tale legge segue quella dello spostamento di Wien. Essa afferma che esiste una particolare relazione tra la temperatura assoluta T di un corpo nero e la lunghezza d'onda λ_max per la quale si ha l'emissione più intensa. Tale relazione è riassunta nell'equazione:

λmaxT=K

È evidente che, essendo temperatura e lunghezza d'onda inversamente proporzionali, all'aumentare di T noteremo che diminuisce la lunghezza d'onda alla quale il corpo emette prevalentemente. Ovvero, aumenta la frequenza di emissione massima.