È possibile prevedere l'andamento della curva analitica data dalla soluzione di Planck osservando ciò che avviene nei casi limite, ovvero quando considerando frequenze molto piccole o molto grandi.

Per ν che tende a 0, la soluzione di Planck si riduce alla legge classica:

u(ν)=8πν2c3⋅k⋅T

Il valore della densità di energia tende chiaramente a 0.
Ecco riconfermato il fatto che la spiegazione classica è un'approssimazione della teoria quantistica per basse frequenze.

Per ν che tende a infinito, la soluzione di Planck è ridotta alla formula:

u(ν,T)=8πc3⋅h⋅ν3⋅e−hνkT

Anche in questo caso è evidente che il valore totale tende a 0.

---

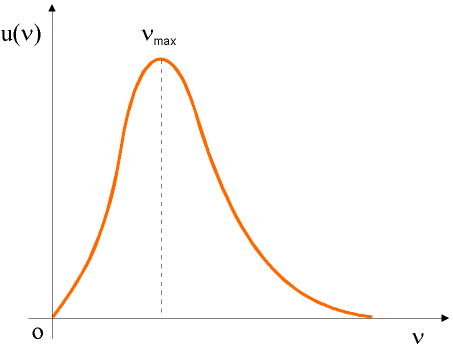
Sapendo che la curva di emissione è sempre positiva ed appurato che essa tende a zero agli estremi (zero e infinito), ne deriva che essa dovrà presentare almeno un massimo.
A quest'ultimo corrisponde una ν particolare, detta ν_max , per la quale si verifica l'emissione massima.