Anche per quanto riguarda il calcolo dell'energia, come abbiamo visto in precedenza, è possibile operare in due modi distinti a seconda si tratti il problema in modo classico oppure quantistico.
In entrambi i casi sarà utilizzata come formula di partenza l'espressione universale ottenuta per la densità di energia, ovvero:

u(ν)=8πν2c3⋅<E>media

Differente sarà tuttavia il modo in cui verrà calcolata l'energia media di ciascun oscillatore.

I fisici giunsero facilmente alla soluzione del problema energetico, ricorrendo al principio fondamentale di equipartizione dell'energia.

<E>=12n⋅k⋅T

Considerando l'onda vibrante come vincolata ad un piano di oscillazione, possiamo affermare che essa si muove su due dimensioni. Pertanto il valore n, che esprime i gradi di libertà del sistema, è uguale a due.

<E>=k⋅T

Ora è sufficiente sostituire quanto ottenuto nell'equazione universale che esprime la densità di energia all'interno della cavità:

u(ν)=8πν2c3⋅k⋅T

Tale equazione è detta di Rayleigh-Jeans, e sorprendentemente risulta in palese contrasto con i dati sperimentali. Confrontando il grafico prodotto da tale legge con le misure fatte in laboratorio, risulta subito evidente che la legge di Rayleigh è accettabile solo per basse frequenze.
Infatti la relazione prevede che la densità di energia cresca con l'aumentare della frequenza, con proporzionalità quadratica. Ma ciò che ne otteniamo, considerando il continuum delle frequenze, è un'energia infinita!

Tale fenomeno è detto catastrofe ultravioletta.

Evidentemente, considerarono i fisici, il principio di equipartizione dell'energia non è applicabile in questo caso; in altre parole, è necessario trovare un metodo alternativo per il calcolo dell'energia media <E>.

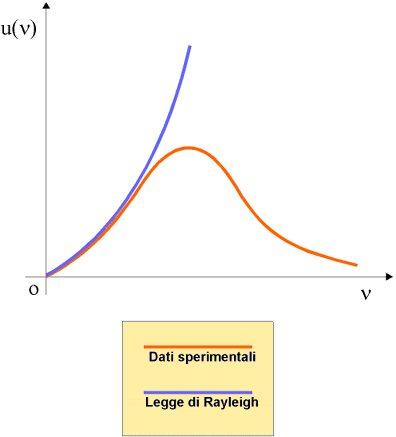
Non è possibile operare un taglio delle frequenze più alte per far coincidere le due curve. In tal caso, infatti, si negherebbe una delle peculiarità essenziali del corpo nero: l'emissione a tutte le frequenze.

Fondamentale per la soluzione del problema energetico fu l'apporto di Max Planck. Egli pose come inequivocabile il fatto che il corpo nero emettesse nel continuum delle frequenze. Ciò che non avveniva nel continuum, bensì per quantità discrete, era l'emissione energetica.
Più semplicemente, ciascun oscillatore nella cavità emetteva energia in quantità discrete, multiple di una quantità minima detta quanto di energia.
Planck, nella legge omonima, espresse tale quantità discreta come il prodotto di una costante h (costante di Planck) per la frequenza propria di un singolo oscillatore.

E=h⋅ν

Partendo dalle considerazioni classiche ed elaborandole sulla base della propria teoria, Planck giunse inoltre a definire la densità di energia relativa al modello di corpo nero.

<E>media=hνehνkT−1

Come è possibile notare, si tratta di un'espressione dell'energia in funzione sia di ν che di T. Inoltre tale equazione si rivela molto flessibile: utilizzando costanti universali (h e k), è infatti utilizzabile per qualsiasi corpo nero, indipendentemente dalla forma della cavità nonché dal materiale di cui è composta.

---

Grazie alla soluzione di Planck, utilizzando la relazione universale per il calcolo della densità di energia è possibile ottenere:

u(ν)=8πhc3⋅ν3ehνkT−1

Tale legge si dimostrò incredibilmente vicina ai risultati sperimentali, descrivendo perfettamente l'andamento della curva di emissione.
Infatti, se si assume che h sia uguale a 6,6 ⋅ 10^-34 J ⋅ s, la curva sperimentale e quella analitica risultano praticamente coincidenti.

Max Planck (Kiel 1858 - Gottinga 1947), fisico tedesco.